An English Painter of the Romantic School Quizlet Chapter Art Chapter 14

4 Sentential Logic

This chapter introduces a logical language called SL. It is a version of sentential logic, because the basic units of the linguistic communication will represent entire sentences.

I. Sentence letters

In SL, capital letters are used to represent basic sentences. Considered merely as a symbol of SL, the letter of the alphabet A could mean whatsoever judgement. And then when translating from English into SL, it is important to provide a symbolization key. The key provides an English language sentence for each judgement letter used in the symbolization.

For instance, consider this argument:

There is an apple on the desk.

If at that place is an apple on the desk, then Jenny made it to class.

.˙. Jenny made information technology to course.

This is obviously a valid statement in English. In symbolizing it, we want to preserve the structure of the argument that makes it valid. What happens if we replace each sentence with a letter? Our symbolization central would await like this:

A: There is an apple on the desk.

B: If there is an apple on the desk-bound, so Jenny made it to class.

C: Jenny made it to class.

We would then symbolize the argument in this style:

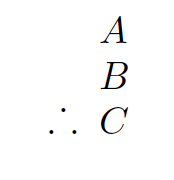
There is no necessary connexion betwixt some sentence A, which could be any sentence, and some other sentences B and C, which could be any sentences. The structure of the argument has been completely lost in this translation.

The of import matter well-nigh the argument is that the 2nd premise is not merely any sentence, logically divorced from the other sentences in the argument. The 2d premise contains the first premise and the decision as parts. Our symbolization key for the statement just needs to include meanings for A and C, and we can build the 2nd premise from those pieces. And then we symbolize the statement this fashion:

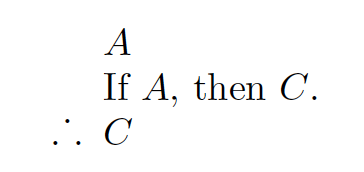
This preserves the structure of the argument that makes it valid, only it still makes use of the English language expression 'If. . . then. . ..' Although we ultimately want to supersede all of the English language expressions with logical note, this is a good offset.

The sentences that can exist symbolized with sentence letters are chosen atomic sentences, because they are the basic building blocks out of which more circuitous sentences can be built. Whatsoever logical structure a judgement might accept is lost when it is translated as an atomic sentence. From the indicate of view of SL, the judgement is just a alphabetic character. Information technology can be used to build more complex sentences, but information technology cannot be taken apart.

There are only xx-half-dozen messages of the alphabet, but there is no logical limit to the number of diminutive sentences. We tin use the aforementioned letter to symbolize dissimilar atomic sentences by adding a subscript, a modest number written afterwards the letter. We could have a symbolization central that looks similar this:

Go on in listen that each of these is a different sentence letter. When there are subscripts in the symbolization key, information technology is important to go along track of them.

II. Connectives

Logical connectives are used to build complex sentences from atomic components. There are five logical connectives in SL. This table summarizes them, and they are explained beneath.

symbol	what it is chosen	what information technology means
¬	negation	'It is non the case that…'
&	conjunction	'Both…and…'
∨	disjunction	'Either…or…"
→	conditional	'If…then…'
↔	biconditional	"…if and but if…'

Negation

Consider how we might symbolize these sentences:

1. Mary is in Barcelona.
2. Mary is not in Barcelona.
3. Mary is somewhere besides Barcelona.

In club to symbolize sentence ane, we will need one judgement letter of the alphabet. Nosotros tin provide a symbolization key:

B: Mary is in Barcelona.

Note that hither we are giving B a different interpretation than we did in the previous department. The symbolization key only specifies what B means in a specific context. Information technology is vital that nosotros continue to use this meaning of B and then long equally we are talking about Mary and Barcelona. Later on, when we are symbolizing dissimilar sentences, we can write a new symbolization key and employ B to hateful something else.

Now, judgement 1 is simply B.

Since judgement 2 is obviously related to the sentence ane, we do not want to introduce a dissimilar judgement letter. To put it partly in English, the sentence ways 'Not B.' In order to symbolize this, we need a symbol for logical negation. We volition use '¬.' Now we can interpret 'Not B' to ¬B.

Sentence iii is about whether or not Mary is in Barcelona, just information technology does not comprise the discussion 'not.' Nevertheless, it is plainly logically equivalent to sentence 2.

They both mean: It is not the example that Mary is in Barcelona. Every bit such, we tin interpret both sentence 2 and judgement 3 as ¬B.

A sentence tin can be symbolized equally ¬Α if information technology can be paraphrased in English language every bit "It is non the case that Α.'

Consider these further examples:

4. The widget can be replaced if it breaks.
5. The widget is irreplaceable.
6. The widget is not irreplaceable.

If we let R hateful 'The widget is replaceable', then sentence 4 tin exist translated as R.

What almost sentence five? Saying the widget is irreplaceable means that it is not the case that the widget is replaceable. And then even though sentence five is non negative in English, we symbolize it using negation as ¬R.

Sentence 6 tin be paraphrased as 'Information technology is not the case that the widget is irreplaceable.' Using negation twice, we interpret this equally ¬¬R. The two negations in a row each work every bit negations, so the judgement means 'It is non the case that. . . information technology is not the case that. . . R.' If you lot retrieve about the sentence in English, it is logically equivalent to sentence four. So when nosotros define logical equivalence in SL, we will make sure that R and ¬¬R are logically equivalent.

More than examples:

7. Elliott is happy.
8. Elliott is unhappy.

If nosotros let H hateful 'Elliot is happy', then we can symbolize judgement 7 as H.

Even so, information technology would be a mistake to symbolize sentence viii as ¬ H . If Elliott is unhappy, then he is not happy— only sentence 8 does not mean the same matter equally 'It is non the case that Elliott is happy.' Information technology could exist that he is not happy but that he is not unhappy either. Perhaps he is somewhere between the two. In club to allow for the possibility that he is indifferent, we would need a new sentence letter to symbolize sentence 8.

For whatsoever sentence A: If A is true, then ¬A is false. If ¬A is true, then A is simulated. Using 'T' for true and 'F' for faux, nosotros can summarize this in a characteristic truth tabular array for negation:

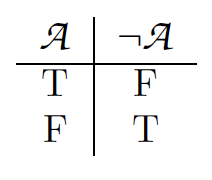
We will discuss truth tables at greater length in the next affiliate.

Conjunction

Consider these sentences:

9.  Adam is athletic.

10. Barbara is athletic.

eleven. Adam is able-bodied, and Barbara is also athletic.

We will need separate judgement letters for 9 and 10, so we define this symbolization key:

A: Adam is athletic.

B: Barbara is athletic.

Sentence 9 can be symbolized as A.

Judgement 10 can be symbolized as B.

Sentence eleven tin can be paraphrased as 'A and B.' In order to fully symbolize this judgement, we need another symbol. Nosotros will use ' & .' Nosotros translate 'A and B' as A & B. The logical connective ' & ' is called CONJUNCTION, and A and B are each called CONJUNCTS.

Notice that we make no endeavour to symbolize 'also' in sentence xi. Words like 'both' and 'too' role to draw our attention to the fact that two things are beingness conjoined. They are non doing whatever farther logical work, so we do non need to represent them in SL.

Some more than examples:

12. Barbara is athletic and energetic.

xiii. Barbara and Adam are both athletic.

xiv. Although Barbara is energetic, she is not athletic.

fifteen. Barbara is athletic, merely Adam is more athletic than she is.

Sentence 12 is obviously a conjunction. The judgement says two things well-nigh Barbara, so in English it is permissible to refer to Barbara simply once. It might be tempting to try this when translating the argument: Since B means 'Barbara is athletic', one might paraphrase the sentences as ' B and energetic.' This would be a mistake. Once we interpret part of a sentence as B , any farther structure is lost. B is an diminutive judgement; it is zippo more than true or false. Conversely, 'energetic' is not a sentence; on its own it is neither true nor simulated. Nosotros should instead paraphrase the judgement equally ' B and Barbara is energetic.' Now we need to add a sentence letter to the symbolization cardinal. Let E mean 'Barbara is energetic.' Now the sentence can be translated as B & Due east .

A sentence tin be symbolized every bit Α & Β if it can be paraphrased in English every bit 'Both Α, and Β.' Each of the conjuncts must exist a sentence.

Sentence xiii says 1 thing about two different subjects. Information technology says of both Barbara and Adam that they are athletic, and in English nosotros utilize the word 'athletic' only once. In translating to SL, information technology is important to realize that the sentence tin be paraphrased every bit, 'Barbara is athletic, and Adam is athletic.' This translates as B & A.

Sentence 14 is a bit more than complicated. The word 'although' sets upwardly a dissimilarity between the offset office of the judgement and the second part. Nevertheless, the judgement says both that Barbara is energetic and that she is not athletic. In order to make each of the conjuncts an diminutive sentence, we demand to replace 'she' with 'Barbara.'

And then we tin paraphrase sentence 14 as, 'Both Barbara is energetic, and Barbara is not able-bodied.' The second conjunct contains a negation, so we paraphrase further: 'Both Barbara is energetic and it is not the instance that Barbara is athletic.' This translates equally E & ¬B.

Sentence xv contains a similar contrastive construction. Information technology is irrelevant for the purpose of translating to SL, so we tin can paraphrase the sentence as 'Both Barbara is able-bodied, and Adam is more than athletic than Barbara.' (Notice that we once more supplant the pronoun 'she' with her name.) How should we translate the second conjunct? We already have the sentence letter A which is almost Adam'south existence able-bodied and B which is about Barbara's being able-bodied, but neither is well-nigh one of them existence more athletic than the other. We need a new sentence alphabetic character. Allow R mean 'Adam is more athletic than Barbara.' Now the sentence translates as B & R.

Sentences that can be paraphrased 'Α, merely Β' or 'Although Α, Β' are best symbolized using conjunction: Α & Β

It is important to continue in mind that the sentence messages A, B, and R are atomic sentences. Considered as symbols of SL, they have no pregnant across beingness true or false. Nosotros take used them to symbolize dissimilar English language sentences that are all near people being athletic, but this similarity is completely lost when nosotros translate to SL. No formal language can capture all the construction of the English linguistic communication, but as long every bit this construction is non important to the argument there is cipher lost past leaving it out.

For any sentences A and B, A & B is true if and only if both A and B are true. Nosotros can summarize this in the characteristic truth table for conjunction:

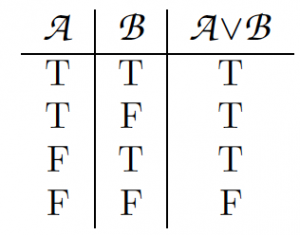
Conjunction is symmetrical considering nosotros tin swap the conjuncts without changing the truth-value of the judgement. Regardless of what A and B are, A & B is logically equivalent to B & A.

Disjunction

Consider these sentences:

16. Either Denison will play golf with me, or he will watch movies.

17. Either Denison or Ellery will play golf game with me.

For these sentences nosotros can utilize this symbolization cardinal:

D: Denison will play golf with me.

E: Ellery will play golf game with me.

M: Denison volition scout movies.

Judgement 16 is 'Either D or M .' To fully symbolize this, we innovate a new symbol. The sentence becomes D ∨ G . The '∨' connective is called DISJUNCTION, and D and Yard are called DISJUNCTS.

Judgement 17 is only slightly more than complicated. There are two subjects, simply the English language sentence only gives the verb one time. In translating, nosotros tin can paraphrase it as. 'Either Denison will play golf with me, or Ellery will play golf with me.' Now it evidently translates as D ∨ East.

A sentence tin be symbolized as Α ∨ Β if it can be paraphrased in English language as 'Either Α, or Β.' Each of the disjuncts must be a judgement.

Sometimes in English language, the word 'or' excludes the possibility that both disjuncts are true. This is chosen an EXCLUSIVE OR. An exclusive or is clearly intended when information technology says, on a eating house carte, 'Entrees come with either soup or salad.' You may take soup; you may take salad; but, if you want both soup and salad, and then you accept to pay extra.

At other times, the word 'or' allows for the possibility that both disjuncts might be true. This is probably the example with sentence 17, higher up. I might play with Denison, with Ellery, or with both Denison and Ellery. Sentence 17 merely says that I will play with at to the lowest degree 1 of them. This is chosen an INCLUSIVE OR.

The symbol '∨' represents an inclusive  or.  And so D  E is true if D is true, if E is true, or if both D and E are truthful. It is fake simply if both D and E are false. We can summarize this with the characteristic truth tabular array for disjunction:

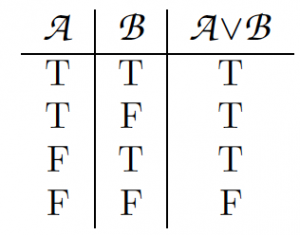
Like conjunction, disjunction is symmetrical. A∨B is logically equivalent to B∨A.

These sentences are somewhat more complicated:

18.    Either you volition not accept soup, or y'all will not have salad.

19.    You volition have neither soup nor salad.

20.    Y'all get either soup or salad, merely not both.

We allow S ₁ hateful that you get soup and S ₂ mean that you get salad.

Sentence xviii can be paraphrased in this way: 'Either it is not the case that you get soup, or it is not the instance that you lot go salad.' Translating this requires both disjunction and negation. It becomes ¬Southward _one ∨ ¬S ₂.

Sentence nineteen as well requires negation. Information technology can be paraphrased as, 'It is not the case that either that you become soup or that you get salad.' Nosotros demand some way of indicating that the negation does not only negate the right or left disjunct, merely rather negates the unabridged disjunction. In order to do this, we put parentheses around the disjunction: 'It is not the case that ( Due south _one ∨ S _ii).' This becomes just ¬( Southward 1 ∨ Southward ii). Observe that the parentheses are doing important work here. The sentence ¬ South ₁ ∨ S _two would mean 'Either y'all will not accept soup, or you lot will have salad.'

Judgement 20 is an exclusive or. We tin can break the sentence into two parts. The first part says that yous get ane or the other. We translate this every bit (Due south ₁ ∨ South _two). The second part says that y'all do not get both. We can paraphrase this as, 'Information technology is non the case both that you get soup and that you get salad.' Using both negation and conjunction, nosotros translate this as ¬(S1 & Southtwo). At present we just need to put the two parts together. Equally we saw above, 'just' tin unremarkably be translated as a conjunction. Sentence twenty tin thus be translated as (Sone ∨ South2) & ¬(Due southone & S2).

Although '∨' is an inclusive or, we can symbolize an exclusive or in SL. We just demand more 1 connective to exercise it.

Conditional

For the post-obit sentences, let R mean 'You lot volition cut the ruddy wire' and B hateful 'The flop will explode.'

21.    If you cut the red wire, and so the flop will explode.

22.    The bomb will explode only if you cut the ruddy wire.

Sentence 21 can be translated partially equally 'If R, and so B.' We will use the symbol '→' to correspond logical entailment. The sentence becomes R → B. The connective is called a CONDITIONAL. The judgement on the left-hand side of the conditional (R in this instance) is chosen the Antecedent. The sentence on the right-manus side (B) is called the Consistent.

Sentence 22 is also a conditional. Since the word 'if' appears in the second half of the sentence, information technology might exist tempting to symbolize this in the same style every bit judgement 21. That would be a fault.

The conditional R → B says that if R were true, then B would also be true. Information technology does non say that your cutting the blood-red wire is the only style that the bomb could explode. Someone else might cut the wire, or the flop might be on a timer. The sentence R → B does not say anything nearly what to expect if R is false. Sentence 22 is different. It says that the only conditions under which the bomb will explode involve your having cut the red wire; i.east., if the bomb explodes, and then you must have cut the wire. Every bit such, sentence 22 should be symbolized equally B → R.

Information technology is of import to remember that the connective '→' says merely that, if the ancestor is true, then the consequent is true. It says nothing about the causal connection betwixt the two events. Translating sentence 22 as B → R does non hateful that the bomb exploding would somehow have caused your cut the wire. Both sentence 21 and 22 advise that, if y'all cut the red wire, your cut the red wire would be the cause of the flop exploding. They differ on the logical connection. If sentence 22 were true, and so an explosion would tell u.s.a.— those of usa safely away from the flop— that you had cutting the reddish wire. Without an explosion, judgement 22 tells the states nothing.

The paraphrased judgement 'Α only if Β' is logically equivalent to 'If Α, then Β.'

'If A then B' means that if A is true then and so is B. So we know that if the ancestor A is true but the consequent B is false, then the conditional 'If A and then B' is false. What is the truth value of 'If A and so B' nether other circumstances? Suppose, for example, that the antecedent A happened to be false. 'If A then B' would then non tell united states anything about the actual truth value of the consequent B, and it is unclear what the truth value of 'If A then B' would exist.

In English language, the truth of conditionals often depends on what would be the case if the ancestor were truthful— fifty-fifty if, every bit a thing of fact, the antecedent is false. This poses a problem for translating conditionals into SL. Considered as sentences of SL, R and B in the higher up examples accept nothing intrinsic to practise with each other. In order to consider what the world would be like if R were true, we would need to analyze what R says about the world. Since R is an atomic symbol of SL, nonetheless, at that place is no farther structure to be analyzed. When nosotros replace a sentence with a sentence letter, nosotros consider it merely as some atomic sentence that might be true or false.

In society to translate conditionals into SL, nosotros will not try to capture all the subtleties of the English language linguistic communication 'If. . . then. . ..' Instead, the symbol '→' will be a textile conditional. This ways that when A is faux, the conditional A→B is automatically true, regardless of the truth value of B. If both A and B are true, so the conditional A → B is true.

In short, A→B is false if and only if A is truthful and B is imitation. Nosotros can summarize this with a characteristic truth tabular array for the conditional.

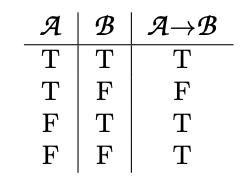
The conditional is asymmetrical. You cannot swap the antecedent and consequent without irresolute the meaning of the sentence, because A→B and B→A are not logically equivalent.

Not all sentences of the form 'If. . . and so. . .' are conditionals. Consider this sentence:

23.    If anyone wants to see me, so I will be on the porch.

If I say this, it means that I will be on the porch, regardless of whether anyone wants to come across me or non— merely if someone did want to see me, then they should await for me at that place. If we allow P mean 'I will be on the porch,' so judgement 23 tin be translated simply as P .

Biconditional

Consider these sentences:

24.    The figure on the board is a triangle only if it has exactly iii sides.

25.    The figure on the lath is a triangle if it has exactly three sides.

26.    The figure on the board is a triangle if and only if information technology has exactly three sides.

Permit T mean 'The effigy is a triangle' and S mean 'The effigy has 3 sides.'

Sentence 24, for reasons discussed above, can be translated as T → Southward.

Sentence 25 is chiefly dissimilar. It can be paraphrased equally, 'If the figure has three sides, then it is a triangle.' So information technology tin exist translated as S → T .

Judgement 26 says that T is truthful if and only if S is true; nosotros can infer S from T , and we tin can infer T from S. This is chosen a biconditional, because it entails the two conditionals South → T and T → S. We will utilize '↔' to correspond the biconditional; sentence 26 tin be translated equally Southward ↔ T .

We could abide without a new symbol for the biconditional. Since sentence 26 means 'T → South and S → T ,' we could translate it as (T → S) & (S → T ). We would demand parentheses to indicate that (T → S) and (S → T ) are carve up conjuncts; the expression T → S & S → T would exist ambiguous.

Considering we could ever write (A → B) & (B → A) instead of A ↔ B, we do not strictly speaking need to introduce a new symbol for the biconditional. Nevertheless, logical languages normally have such a symbol. SL will have one, which makes information technology easier to translate phrases like 'if and just if.

A ↔ B is truthful if and merely if A and B accept the same truth value. This is the feature truth table for the biconditional:

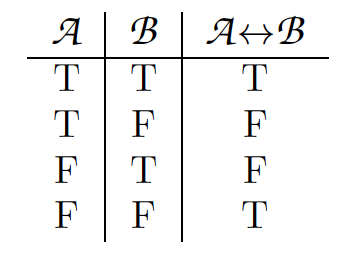
3. Other symbolization

Nosotros take at present introduced all of the connectives of SL. We can use them together to translate many kinds of sentences. Consider these examples of sentences that utilize the English-linguistic communication connective 'unless':

27.    Unless you wearable a jacket, y'all will catch cold.

28.    You will catch cold unless yous wear a jacket.

Let J hateful 'Y'all volition wear a jacket' and let D mean 'You will catch a cold.'

Nosotros can paraphrase sentence 27 as 'Unless J , D.' This ways that if you practise not habiliment a jacket, then yous will grab common cold; with this in heed, we might translate information technology as ¬J → D. It also means that if y'all do non grab a cold, then you must have worn a jacket; with this in mind, we might interpret it as ¬D → J .

Which of these is the right translation of judgement 27? Both translations are correct, because the two translations are logically equivalent in SL.

Sentence 28, in English, is logically equivalent to judgement 27. It can be translated equally either ¬J → D or ¬D → J .

When symbolizing sentences like sentence 27 and sentence 28, information technology is easy to get turned effectually. Since the provisional is non symmetric, it would be wrong to translate either judgement every bit J →¬D. Fortunately, there are other logically equivalent expressions. Both sentences mean that you will wear a jacket or— if you do not wear a jacket— then you volition catch a cold. And so nosotros can translate them equally J ∨ D. (You might worry that the 'or' here should exist an exclusive or. Nonetheless, the sentences practise non exclude the possibility that you might both vesture a jacket and catch a cold; jackets do not protect you from all the possible ways that you might catch a common cold.)

If a sentence can exist paraphrased as "Unless Α, Β,' then information technology tin can be symbolized as Α ∨ Β.

IV. Sentences of SL

The sentence 'Apples are red, or berries are blue' is a sentence of English, and the sentence '(A ∨ B)' is a judgement of SL. Although we can place sentences of English when we encounter them, nosotros practice not have a formal definition of 'sentence of English'. In SL, information technology is possible to formally define what counts as a judgement. This is one respect in which a formal language like SL is more precise than a natural language like English.

It is important to distinguish between the logical language SL, which we are developing, and the language that nosotros use to talk about SL. When we talk well-nigh a language, the language that we are talking about is called the object language. The language that we utilize to talk about the OBJECT LANGUAGE is called the METALANGUAGE.

The object linguistic communication in this chapter is SL. The metalanguage is English— not conversational English, just English language supplemented with some logical and mathematical vocabulary. The sentence '(A ∨ B)' is a judgement in the object linguistic communication, because it uses only symbols of SL. The discussion 'sentence' is not itself part of SL, however, and then the sentence 'This expression is a sentence of SL' is not a sentence of SL. It is a sentence in the metalanguage, a judgement that we use to talk about SL.

In this section, we will give a formal definition for 'sentence of SL.' The definition itself will be given in mathematical English, the metalanguage.

Expressions

At that place are three kinds of symbols in SL:

sentences letters with subscripts, equally needed	A, B, C,…,Z or as needed: A1,B1, Z1, Aii, A25, J375,…
connectives	¬, &, ∨, →, ↔
parentheses	( , )

We define an EXPRESSION of SL every bit any string of symbols of SL. Have any of the symbols of SL and write them downwards, in any order, and you lot have an expression.

Well-formed formulae

Since any sequence of symbols is an expression, many expressions of SL will be gobbledegook. A meaningful expression is chosen a well-formed formula. It is common to use the acronym wff ; the plural is wffs.

Obviously, individual judgement letters like A and M ₁₃ will exist wffs. We tin can form farther wffs out of these by using the various connectives. Using negation, we can get ¬A and ¬G _xiii. Using conjunction, we can get A & K ₁₃, Grand ₁₃ & A, A & A, and G ₁₃ & G ₁₃. Nosotros could also apply negation repeatedly to become wffs ¬¬A or apply negation forth with conjunction to get wffs similar ¬(A & G ₁₃) and (G ₁₃ & M ₁₃). The possible combinations are endless, even starting with only these two sentence messages, and there are infinitely many sentence letters. And so there is no point in trying to list all the wffs.

Instead, nosotros will depict the process by which wffs can be constructed. Consider negation: Given whatsoever wff A of SL, A is a wff of SL. It is of import here that A is not the sentence alphabetic character A. Rather, it is a variable that stands in for any wff at all. Discover that this variable A is not a symbol of SL, so A is not an expression of SL. Instead, it is an expression of the metalanguage that allows us to talk almost infinitely many expressions of SL: all of the expressions that start with the negation symbol. Because A is role of the metalanguage, it is called a metavariable.We tin can say similar things for each of the other connectives. For example, if A and B are wffs of SL, then (A & B) is a wff of SL. Providing clauses like this for all of the connectives, we arrive at the post-obit formal definition for a well-formed formula of SL:

1.    Every diminutive sentence is a wff.

2.    If A is a wff, and then ¬A is a wff of SL.

3.    If A and B are wffs, then (A & B) is a wff.

four.    If A and B are wffs, so (A ∨ B) is a wff.

5.    If A and B are wffs, and then (A → B) is a wff.

vi.    If A and B are wffs, so (A ↔ B) is a wff.

7.    All and only wffs of SL can be generated by applications of these rules.

Notice that nosotros cannot immediately utilise this definition to see whether an arbitrary expression is a wff.  Suppose nosotros want to know whether or not D is a wff of SL. Looking at the second clause of the definition, nosotros know that¬¬¬D is a wff if ¬¬D is a wff. So now nosotros need to ask whether or not ¬¬D is a wff. Once again looking at the second clause of the definition, D is a wff if D is. Once again, D is a wff if D is a wff. At present D is a sentence letter of the alphabet, an atomic sentence of SL, so we know that D is a wff by the showtime clause of the definition. So for a compound formula like D , we must employ the definition repeatedly. Somewhen nosotros arrive at the atomic sentences from which the wff is congenital up.

Definitions like this are called recursive. Recursive definitions begin with some specifiable base elements and define means to indefinitely compound the base elements. Simply as the recursive definition allows complex sentences to be built up from simple parts, you tin use information technology to decompose sentences into their simpler parts. To determine whether or not something meets the definition, you may have to refer dorsum to the definition many times.

The connective that y'all look to kickoff in decomposing a sentence is chosen the Main LOGICAL OPERATOR of that judgement. For example: The main logical operator of ¬(E ∨ (F → G)) is negation, ¬. The main logical operator of (¬East ∨ (F → G)) is disjunction, ∨.

Sentences

Call back that a sentence is a meaningful expression that can be true or false. Since the meaningful expressions of SL are the wffs and since every wff of SL is either true or false, the definition for a sentence of SL is the same equally the definition for a wff. Not every formal language will have this nice characteristic. In the language QL, which is developed later in the book, there are wffs which are not sentences.

The recursive structure of sentences in SL volition be important when nosotros consider the circumstances under which a particular judgement would exist true or false. The sentence D is true if and only if the sentence D is false, and so on through the structure of the sentence until nosotros arrive at the atomic components: ¬¬¬D is true if and only if the diminutive sentence D is false. We will return to this indicate in the adjacent chapter.

Notational conventions

A wff like (Q & R) must be surrounded past parentheses, because we might apply the definition again to employ this as role of a more complicated judgement. If we negate (Q & R), we get (Q & R). If we just had Q & R without the parentheses and put a negation in front of information technology, we would accept Q & R. It is most natural to read this as meaning the aforementioned thing as ( Q & R), something very different than (Q & R). The judgement (Q & R) means that it is not the case that both Q and R are true; Q might be imitation or R might be simulated, but the sentence does non tell us which. The sentence (¬Q & R) means specifically that Q is simulated and that R is true. As such, parentheses are crucial to the meaning of the sentence.

And then, strictly speaking, Q & R without parentheses is not a judgement of SL. When using SL, still, we volition ofttimes be able to relax the precise definition so equally to brand things easier for ourselves. Nosotros volition practise this in several ways.

Offset, we understand that Q & R means the same thing as (Q & R). As a affair of convention, we can go out off parentheses that occur around the entire judgement.

Second, information technology tin can sometimes exist confusing to look at long sentences with many, nested pairs of parentheses. We prefer the convention of using foursquare brackets '[' and ']' in identify of parenthesis. There is no logical difference between (P ∨ Q) and [P ∨ Q], for example. The unwieldy sentence (((H → I) ∨ (I → H)) & (J ∨ K)) could be written in this way: [(H → I) ∨ (I → H)] & (J ∨ Thousand).

Third, we will sometimes want to translate the conjunction of 3 or more sentences. For the sentence 'Alice, Bob, and Candice all went to the party', suppose nosotros let A mean 'Alice went', B mean 'Bob went', and C mean 'Candice went.' The definition but allows us to grade a conjunction out of ii sentences, so we tin translate it as (A & B) & C or as A & (B & C). There is no reason to distinguish between these, since the two translations are logically equivalent. In that location is no logical difference between the first, in which (A & B) is conjoined with C, and the second, in which A is conjoined with (B & C). Then we might as well just write A & B & C. Every bit a affair of convention, we tin exit out parentheses when we conjoin three or more sentences.

Fourth, a like situation arises with multiple disjunctions. 'Either Alice, Bob, or Candice went to the party' can be translated every bit (A ∨ B) ∨ C or equally A ∨(B ∨ C). Since these two translations are logically equivalent, we may write A ∨ B ∨ C.

These latter two conventions just apply to multiple conjunctions or multiple disjunctions. If a serial of connectives includes both disjunctions and conjunctions, then the parentheses are essential; as with (A & B) C and A & (B C). The parentheses are besides required if there is a series of conditionals or biconditionals; as with (A → B) → C and A ↔ (B ↔ C).

Nosotros take adopted these iv rules equally notational conventions, not equally changes to the definition of a sentence. Strictly speaking, A B C is still not a sentence. Instead, it is a kind of autograph. Nosotros write information technology for the sake of convenience, but we really mean the sentence (A ∨ (B ∨ C)).

If we had given a different definition for a wff, and so these could count equally wffs. We might have written rule 3 in this way: "If A, B, . . . Z are wffs, then ( A & B & . . . & Z ), is a wff." This would arrive easier to interpret some English language sentences, but would have the toll of making our formal language more complicated. We would accept to continue the complex definition in mind when nosotros develop truth tables and a proof system. Nosotros want a logical language that is expressively simple and allows us to translate easily from English, but nosotros also want a formally simple linguistic communication. Adopting notational conventions is a compromise betwixt these two desires.

Five. Practise Exercises

* Part A Using the symbolization fundamental given, translate each English language-language sentence into SL.

Yard: Those creatures are men in suits.

C: Those creatures are chimpanzees.

Grand: Those creatures are gorillas.

1. Those creatures are not men in suits.
2. Those creatures are men in suits, or they are non.
3. Those creatures are either gorillas or chimpanzees.
4. Those creatures are neither gorillas nor chimpanzees.
5. If those creatures are chimpanzees, then they are neither gorillas nor men in suits.
6. Unless those creatures are men in suits, they are either chimpanzees or they are gorillas.

Part B Using the symbolization central given, translate each English language-language sentence into SL.

A: Mister Ace was murdered.

B: The butler did information technology.

C: The cook did information technology.

D: The Duchess is lying.

E: Mister Border was murdered.

F: The murder weapon was a frying pan.

1. Either Mister Ace or Mister Edge was murdered.
2. If Mister Ace was murdered, then the cook did it.
3. If Mister Edge was murdered, then the cook did not practise it.
4. Either the butler did information technology, or the Duchess is lying.
5. The melt did it only if the Duchess is lying.
6. If the murder weapon was a frying pan, and so the culprit must have been the cook.
7. If the murder weapon was not a frying pan, so the culprit was either the melt or the butler.
8. Mister Ace was murdered if and only if Mister Border was non murdered.
9. The Duchess is lying, unless it was Mister Border who was murdered.
10. If Mister Ace was murdered, he was washed in with a frying pan.
11. Since the cook did information technology, the butler did not.
12. Of course the Duchess is lying!

* Part C Using the symbolization key given, interpret each English-language sentence into SL.

E1: Ava is an electrician.

E2: Harrison is an electrician.

F1: Ava is a fire-eater.

Fii: Harrison is a firefighter.

S1: Ava is satisfied with her career.

Due south2: Harrison is satisfied with his career.

1. Ava and Harrison are both electricians.
2. If Ava is a fireman, so she is satisfied with her career.
3. Ava is a firefighter, unless she is an electrician.
4. Harrison is an unsatisfied electrician.
5. Neither Ava nor Harrison is an electrician.
6. Both Ava and Harrison are electricians, but neither of them find it satisfying.
7. Harrison is satisfied just if he is a firefighter.
8. If Ava is not an electrician, then neither is Harrison, but if she is, and so he is too.
9. Ava is satisfied with her career if and but if Harrison is not satisfied with his.
10. If Harrison is both an electrician and a fire-eater, then he must be satisfied with his piece of work.
11. Information technology cannot be that Harrison is both an electrician and a firefighter.
12. Harrison and Ava are both firefighters if and but if neither of them is an electrician.

* Part D Give a symbolization primal and symbolize the post-obit sentences in SL.

1. Alice and Bob are both spies.
2. If either Alice or Bob is a spy, then the code has been broken.
3. If neither Alice nor Bob is a spy, then the code remains unbroken.
4. The German embassy will be in an uproar, unless someone has broken the code.
5. Either the code has been cleaved or it has not, just the German embassy will be in an uproar regardless.
6. Either Alice or Bob is a spy, only not both.

Function East Give a symbolization primal and symbolize the following sentences in SL.

1. If Gregor plays get-go base, then the team will lose.
2. The team will lose unless there is a miracle.
3. The squad will either lose or information technology won't, but Gregor will play first base regardless.
4. Gregor'south mom will bake cookies if and merely if Gregor plays first base.
5. If at that place is a miracle, then Gregor's mom volition not broil cookies.

Office F For each argument, write a symbolization key and interpret the argument besides as possible into SL.

1. If Dorothy plays the piano in the morning time, then Roger wakes up cranky. Dorothy plays piano in the morning unless she is distracted. And so if Roger does not wake up cranky, and so Dorothy must be distracted.
2. It volition either rain or snow on Tuesday. If it rains, Neville will be pitiful. If it snows, Neville will be common cold. Therefore, Neville will either be lamentable or common cold on Tuesday.
3. If Zoog remembered to do his chores, so things are clean but not keen. If he forgot, then things are peachy simply not clean. Therefore, things are either slap-up or clean— simply not both.

* Part G For each of the following: (a) Is information technology a wff of SL? (b) Is information technology a judgement of SL, assuasive for notational conventions?

1. (A)
2. J374 ∨ ¬J374
3.  ¬¬¬¬F
4. ¬ & S
5. (G & ¬Thou)
6. A → A
7. (A → (A & ¬F )) ∨ (D ↔ East)
8. [(Z ↔ S) → Due west ] & [J ∨ X]
9. (F ↔ ¬D → J ) ∨ (C & D)

Part H

1. one. Are at that place whatever wffs of SL that contain no judgement letters? Why or why not?
2. 2. In the chapter, we symbolized an exclusive or using ∨, & , and ¬. How could you translate an exclusive or using only two connectives? Is there whatsoever fashion to translate an exclusive or using only one connective?

linnafteneirs.blogspot.com

Source: https://open.library.okstate.edu/criticalthinking/chapter/chapter-4-sentential-logic/

Share this post